Contents

1 What is Polyhedral Computation FAQ?

This is an FAQ to answer some basic questions arising from certain geometric computation in general dimensional (mostly Euclidean) space. The main areas to be covered are the convex hull computation of a finite point set, the vertex enumeration for a convex polytope, the computation of Voronoi diagram and Delaunay triangulation, in $R^d$. We illustrate typical solution processes with small examples and publicly available codes such as cddlib [Fuka] and lrslib [Avi].

It is still incomplete and perhaps contains a number of typos and mistakes at this moment, but I will try to make it as complete as possible for the primary purposes.

We do not intend to discuss techniques and algorithms specially designed for particular dimensions (e.g. 2D and 3D). For those interested primarily in geometric computation in lower dimensions (e.g. 2 and 3) should consult the comp.graphics.algorithms FAQ [O’R] as well as a handbook of discrete and computational geometry [Ge97].

Please note that the Polyhedral Computation FAQ is available from [Fukb] in pdf format. The html version might become available as well, and it has an advantage of having html links within the documents. Yet, one has to be aware of the fact that some conversion errors exist that give wrong equation numberings and missing figures. Please consider the pdf version as the most reliable source.

We do not provide any proofs for the stated results in this document. The basic theory and computational algorithms on convex polyhedra are presented with rigorous proofs in the textbook [Fuk20b].

To refer to this document, please use

Komei Fukuda
Polyhedral computation FAQ
ETH Zurich, Switzerland
fukuda@math.ethz.ch
https://cddlib.github.io/polyhedral_faq/ or (less up to date)
https://people.inf.ethz.ch/fukudak/.

Please send your comments to the email address above.

2 Convex Polyhedron

2.1 What is convex polytope/polyhedron?

A subset $P$ of $R^d$ is called a convex polyhedron if it is the set of solutions to a finite system of linear inequalities, and called convex polytope if it is a convex polyhedron and bounded. When a convex polyhedron (or polytope) has dimension $k$, it is called a $k$-polyhedron ($k$-polytope). For the sequel, we might omit convex for convex polytopes and polyhedra, and call them simply polytopes and polyhedra.

2.2 What are the faces of a convex polytope/polyhedron?

Let $P$ be a convex $d$-polyhedron (or $d$-polytope) in $R^d$.

For a real $d$-vector $c$ and a real number $d$, a linear inequality $c^{T}x\le d$ is called valid for $P$ if $c^{T}x\le d$ holds for all $x\in P$. A subset $F$ of a polyhedron $P$ is called a face of $P$ if it is represented as

for some valid inequality $c^{T}x\le d$. By this definition, both the empty set $\varnothing$ and the whole set $P$ are faces. These two faces are called improper faces while the other faces are called proper faces.

We can define faces geometrically. For this, we need to define the notion of supporting hyperplanes. A hyperplane $h$ of $R^d$ is supporting $P$ if one of the two closed halfspaces of $h$ contains $P$. A subset $F$ of $P$ is called a face of $P$ if it is either $\varnothing$, $P$ itself or the intersection of $P$ with a supporting hyperplane.

The faces of dimension $0$, $1$, $\dim <!--\; FUNCTION\; APPLICATION\; -->(P)-2$ and $\dim <!--\; FUNCTION\; APPLICATION\; -->(P)-1$ are called the vertices, edges, ridges and facets, respectively. The vertices coincide with the extreme points of $P$ which are defined as points which cannot be represented as convex combinations of two other points in $P$. When an edge is not bounded, there are two cases: either it is a line or a half-line starting from a vertex. A half-line edge is called an extreme ray.

2.3 What is the face lattice of a convex polytope

The face poset $\mathit{FL}(P)$ of a convex polyhedron is the set of all faces of $P$ ordered by set inclusion. Two polytopes are called isomorphic if their face posets are isomorphic. The face poset of a convex polytope is a lattice.

The face poset of a convex polyhedron is sometimes referred to as the combinatorial structure of the polyhedron. Thus the expression “two polyhedra are combinatorially equal” means they are isomorphic.

2.4 What is a dual of a convex polytope?

For a convex polytope $P$, any convex polytope $P^{\prime }$ with $\mathit{FL}(P^{\prime })$ anti-isomorphic to $\mathit{FL}(P)$ (i.e. “upside-down” of $\mathit{FL}(P)$) is called a (combinatorial) dual of $P$. By the definition, a dual polytope has the same dimension as $P$. The duality theorem states that every convex polytope admits a dual.

When $P$ contains the origin in its interior, the polytope $P^{\ast }$ is called the polar of $P$. One can easily show that

where $V(P)$ denote the set of vertices of $V$, and this inequality (H-) representation of $P^{\ast }$ is minimal (i.e. contains no redundant inequalities).

2.5 What is simplex?

A subset $P$ of $R^d$ is called a $k$-simplex ($k=0,1,2,\dots <!--\; FUNCTION\; APPLICATION\; -->$) if it is the convex hull of $k+1$ affinely independent points. It has exactly $k+1$ vertices and $k+1$ facets. A simplex is a $k$-simplex for some $k$.

Simplices are selfdual, i.e. a dual (see 2.4) of a simplex is again a simplex.

2.6 What is cube/hypercube/cross polytope?

A subset $P$ of $R^d$ is called a unit $d$-cube if it is the convex hull of all $2^d$ points with components $0$ or $1$. It has exactly $2^d$ vertices and $2d$ facets. A cube or hypercube is a convex polytope which is isomorphic to the $d$-cube for some $d$.

A dual (see 2.4) of a cube is called a cross polytope.

2.7 What is simple/simplicial polytope?

A $d$-polytope is called simple if each vertex is contained in exactly $d$ facets. A $d$-polytope is called simplicial if each facet contains exactly $d$ vertices. By definition, a dual of simple (simlicial) polytope is simplicial (simple, respectively). Every facet of a simplicial $d$-polytope is a $(d-1)$-simplex. Each vertex of a simple $d$-polytope is contained in exactly $d$-edges.

A $d$-cube is a simple polytope and a $d$-simplex is both simple and simplicial.

2.8 What is 0-1 polytope?

A polytope in $R^d$ is called 0-1 if all its vertices are in ${\{0,1\}}^d$. In other words, a 0-1 polytope is the convex hull of a subset of the $2^d$ point set ${\{0,1\}}^d$, for some $d\ge 0$.

2.9 What is the best upper bound of the numbers of $k$-dimensional faces of a $d$-polytope with $n$ vertices?

Let $f_k(P)$ denote the number of $k$-faces of a $d$-polytope $P$, for $k=0,1,\dots <!--\; FUNCTION\; APPLICATION\; -->,d$.

The exact upper bound for $f_k$ in terms of $f_0$ and $d$. is known, thanks to McMullen’s upper bound theorem.

The convex hull of distinct $n$ points on the moment curve $\{m(t)=(t^1,t^2,\dots <!--\; FUNCTION\; APPLICATION\; -->,t^d):t\in R\}$ in $R^d$ is known as a cyclic polytope. It is known that its combinatorial structure (i.e. its face lattice, see Section 2.3) is uniquely determined by $n$ and $d$. Thus we often write $C(d,n)$ to denote any such cyclic $d$-polytope with $n$ vertices.

McMullen’s Upper Bound Theorem shows that the maximum of $f_k(P)$ is attained by the cyclic polytopes.

The number of $k$-faces of a cyclic polytope $C(d,n)$ can be explicitely given and thus one can evaluate the order of the upper bound in terms of $n$ and $d$.

For example,

The upper bound theorem can be written in dual form which gives, for example, the maximum number of vertices in a $d$-polytope with $m$ facets.

The original proof of the Upper Bound Theorem is in [McM70, MS71]. There are different variations, see [Kal97, Mul94, Zie94]. The textbook [Fuk20b, Chap 6] presents a detailed proof based on [Kal97] which is beautiful but has a little typo.

2.10 What is convex hull? What is the convex hull problem?

For a subset $S$ of $R^d$, the convex hull $\mathit{conv}(S)$ is defined as the smallest convex set in $R^d$ containing $S$.

The convex hull computation means the “determination” of $\mathit{conv}(S)$ for a given finite set of $n$ points $S=\{p^1,p^2,\dots <!--\; FUNCTION\; APPLICATION\; -->,p^n\}$ in $R^d$.

The usual way to determine $\mathit{conv}(S)$ is to represent it as the intersection of halfspaces, or more precisely, as a set of solutions to a minimal system of linear inequalities. This amounts to output a matrix $A\in R^{m\times d}$ and a vector $b\in R^m$ for some $m$ such that $\mathit{conv}(S)=\{x|Ax\le b\}$. When $\mathit{conv}(S)$ is full-dimensional, each (nonredundant) inequality corresponds to a facet of $\mathit{conv}(S)$. Thus the convex hull problem is also known as the facet enumeration problem, see Section 2.12.

Some people define the convex hull computation as the determination of extreme points of $\mathit{conv}(S)$, or equivalently that of redundant points in $S$ to determine $\mathit{conv}(S)$. This is much simpler computation than our convex hull problem. In fact, this can be done by solving $O(n)$ linear programs and thus polynomially solvable, see Section 2.19 and 2.20. It is better to name this as the “redundancy removal for a point set $S$”.

2.11 What is the Minkowski-Weyl theorem for convex polyhedra?

The Minkowski-Weyl Theorem states every polyhedron is finitely generated and every finitely generated set is a polyhedron. More precisely, for two subsets $P$ and $Q$ of $R^d$, $P+Q$ denotes the Minkowski sum of $P$ and $Q$:

Thus, every polyhedron has two representations of type (a) and (b), known as (halfspace) H-representation and (vertex) V-representation, respectively. A polyhedron given by H-representation (V-representation) is called H-polyhedron (V-polyhedron).

2.12 What is the vertex enumeration problem, and what is the facet enumeration problem?

When a polyhedron $P$ in $R^d$ has at least one extreme point and full dimensional, both representations (a) and (b) in Miknowski-Weyl Theorem 5 are unique up positive multiples of each inequality and ray $r_j$.

Under these regularity conditions, the conversions between the H-representation and the V-representation are well-defined fundamental problems. The transformation (a) to (b) is known as the vertex enumeration and the other (b) to (a) is known as the facet enumeration. When $P$ is in addition bounded (i.e. polytope), the facet enumeration problem reduces to what we call the convex hull problem, see 2.10.

If a given polyhedron does not satisfy the assumptions, it is easy to transform the polyhedron to an isomorphic lower dimensional polyhedron satisfying the assumptions.

There are easy (nondegenerate) cases and difficult (degenerate) cases. For simplicity, we assume that $P$ is bounded (i.e. polytope). The vertex enumeration is called nondegenerate if there is no point $x\in R^d$ which satisfies $d+1$ given inequalities with equality, and degenerate otherwise. The facet enumeration is called nondegenerate if there is no $(d+1)$ given points which are on a common hyperplane, and degenerate otherwise.

2.13 How can one enumerate all faces of a convex polyhedron?

Let $P$ be a convex polytope in $R^d$. One can extend the discussion below for the unbounded case (polyhedron) by adding a face at infinity, but for simplicity we assume $P$ is bounded.

First of all the answer does not depend on how $P$ is given. The problem for H-polytopes is equivalent to the one for V-polytopes by duality. See Sections 2.11 and 2.4.

There are algorithms (e.g. [Rot92, Sei86, FLM97] ) that can generate all faces from a V-representation or from a H-rerepsentation. Perhaps the backtrack algorithm [FLM97] is easiest to implement and works directly for the unbounded case. It is also a compact polynomial algorithm (see 2.15) and thus needs little space to run. Algorithms that need to store all faces during computation tend to be too complicated to implement, because one needs to manage a complex data structure of faces and their incidences.

Another approach to generate all faces consists of two steps.

(1)

Firstly compute the second representation by a representation conversion algorithm.

(2)

Secondly use a combinatorial method to genrate all faces.

The first part is discussed in Section 2.15 and Section 5 presents some existing implementation. The second part can be done efficiently by purely combinatorial computation, see [FR94]. As explained in [FR94], when the polytope is simple (simplicial), the face listing without duplication can be done implicitely by sorting the vertices (the facets) by a generic linear function (a generic line through an interior point).

2.14 What computer models are appropriate for the polyhedral computation?

There are two important computational models, the unit cost RAM (random access machine) and the Turing machine. The essential difference is that the Turing machine uses the binary representations of numbers and the computational time is measured precisely down to the number of (unit cost) bit operations. I believe that the RAM model, in which each elementary arithmetic operation takes a unit time and each integer number takes a unit space, is the standard model for the polyhedral computation. This model, despite its simplicity, often illuminates the critical parts of an algorithm and thus reflects the actual computation well. Of course, ignoring the number of bits of a largest number arising in the computation is dangerous, if one does not control the exponential growth of bit lengths of the numbers (in terms of the input bit length). This warning should be always kept in mind to design a good implementation. Furthermore, there are certain cases in which we need to use the Turing complexity. For example, all known “polynomial” algorithms for the linear programming (see Section 4) are Turing polynomial but not RAM polynomial. We may avoid this problem by pretending that there were a RAM polynomial algorithm for LP. After all, we (those interested in geometric computation) are interested in an analysis which reflects the reality and the simplex method for LP is practically a RAM polynomial (or equivalently, strongly polynomial) method. We refer to the recent book [Yap00] for further discussions.

2.15 How do we measure the complexity of a convex hull algorithm?

To answer this question, we assume the unit cost RAM model, where the computational time is essentially the number of elementary arithmetic operations and the storage for any integer number takes a unit space. See Section 2.14.

There are two approaches to evaluate the complexity of a given convex hull algorithm.

Let $\alpha$ be an algorithm which computes a minimal inequality description $P=\{x:\mathit{Ax}\le b\}$ of a full-dimensional convex polytope $P=\mathit{conv}(S)$ for a given point set $S$ in $R^d$ with $n=\left|S\right|$. Let $m$ denote the number of inequalities in the output $\mathit{Ax}\le b$.

(One can interprete the discussion here in dual setting: consider $\alpha$ as an algorithm to compute all vertices $S^{\prime }$ of a convex polytope $P=\{x:A^{\prime }x\le b^{\prime }\}$ with $n$ inequaities with $m$ vertices.)

First of all, most people agree that the efficiency of computing the convex hull should be measured at least by the critical input parameters $d$ and $n$. Some people like to see the complexity by fixing $d$ to constant, but it is always better to evaluate in terms of $d$ as well, and fix it later.

The first measure, often employed by computational geometers, is to bound the worst case running time of an algorithm $\alpha$ for any input with $n$ points in $R^d$. For example, if $\alpha$ is of $O(d!n^d)$, then it means $\alpha$ terminates in time $O(d!n^d)$ for ANY input of $n$ points in dimension $d$. Also, when one set $d$ to be fixed (constant), such an algorithm is said to have time complexity $O(n^d)$, since $d!$ is simply a constant. We may call this worst-case-input measure. For fixed dimension, there is an optimum algorithm [Cha93] for the convex hull in terms of the worst-case-input measure, that runs in time $O(n^{\lfloor d∕2\rfloor })$ for $d\ge 4$. It cannot be better because the largest output is of the same order by the upper bound theorem (Theorem 2).

The worst-case-input measure is quite popular, but it might be little misleading. For example, suppose algorithms $\alpha$ and $\beta$ are of time complexity $O(n^d)$ and $O(n^{2d})$, respectively. Then by this measurement, the algorithm $\alpha$ is superior to $\beta$.

Here is a potentially serious problem with this worst-case-input measure. Above, it is still possible that $\alpha$ takes worst-case time $n^d$ for ALL input of $n$ points in $R^d$, and $\beta$ takes time proportional to some polynomial function of $n,d,m$. Note that the number $m$ of inequalities varies wildly from $O(1)$ to $O(n^{\lfloor d∕2\rfloor })$, even for fixed $d$ (by the upper bound theorem Theorem 2 and (1)). This diversity is just too big to be ignored if $d\ge 4$. Furthermore, the input data leading to the worst-case output hardly occurs in practice. In fact, for the random spherical polytope, the expected size of $m$ is linear in $n$, see Section 2.16. While the worst-case-input optimal algorithm [Cha93] is a remarkable theoretical achievement, we are still very far from knowing the best ways to compute the convex hull for general dimensions.

In order to circumvent this pitfall, one can use a measure using all key variables $d,n,m$. Or more generally, one can measure the time complexity in terms of both the size of input and the size of output. We say an algorithm $\alpha$ is polynomial if it runs in time bounded by a polynomial in $d,n,m$. This polynomiality coincides with the usual polynomiality when the output size is polynomially bounded by the size of input.

Under the nondegeneracy assumption (see 2.12), there is a polynomial algorithm for the convex hull problem. Few of the earlier polynomial algorithms are pivot-based algorithms [CCH53, Dye83] solving the problem in dual form (the vertex enumeration problem) and a wrapping algorithm [CK70]. A more recent algorithm [AF92] based on reverse search technique [AF96] is not only polynomial but compact at the same time. Here, we say an algorithm is compact if its space complexity is polynomial in the input size only.

In the general case, there is no known polynomial algorithm. The paper [ABS97] is an excellet article presenting how various algorithms fail to be polynomial, through ingenious constructions of “nasty” polytopes.

2.16 How many facets does the average polytope with $n$ vertices in $R^d$ have?

Clearly we need to define a probability distribution of points to answer the question.

Perhaps the most interesting describution for which the answer is known is the uniform distribution on the unit sphere $S^{d-1}$. The results of Buchta et al [BMT85] show that the expected number of facets is $f(d,n)=\frac{2}{d}\gamma ({(d-1)}^2)\gamma {(d-1)}^{-(d-1)}(n+o(1))$ assymtotically with $n\to \infty$. The important fact is that it depends linearly on $n$ essentially. Here the function $\gamma (p)$ is defined recursively by

Just to see how large the slope $g(d)=\frac{2}{d}\gamma ({(d-1)}^2)\gamma {(d-1)}^{-(d-1)}$ of this “linear” function in $n$ is, we calculate it for $d\le 15$:

2.17 How many facets can a 0-1 polytope with $n$ vertices in $R^d$ have?

Let $f(d)$ denote the maximum number of facets of a 0-1 polytope in $R^d$. The question such as “is this function bounded by an exponential in $d$?” was open just until recently. The negative answer was given by Bárány and Pór who proved the superexponential behavior of $f(d)$.

This is a recent breakthrough in the theory of 0-1 polytopes.

2.18 How hard is it to verify that an H-polyhedron $P_H$ and a V-polyhedron $P_V$ are equal?

This is a fundamental complexity question associated with the Minkowski-Weyl theorem (Theorem 5). This problem, known as the polyhedral verification problem was first posed by L. Lovasz (see [Sey94]).

To simplify our discussion, let us assume $P_H$ and $P_V$ are bounded and thus polytopes. Also we may assume that the given representations contain no redundant data, since removing redundancies is just a matter of solving linear programs, see Sections 2.19 and 2.21.

The verification consists of two questions, “is $P_V\subseteq P_H$?” and “is $P_H\subseteq P_V$?” The first question is easy to answer by just checking whether each generator (vertex) of $P_V$ satisfies the H-representation of $P_H$. The second question is known to be coNP-complete, due to [FO85]. (It is not hard to see that it belongs to coNP, since the negative answer to the question has a succinct certificate, a vertex $v$ of $P_H$ and a hyperplane separating $v$ from $P_V$.) Yet, the complexity of the second question, when the first question has the positive answer, is not known.

It is possible to prove that the polynomial solvability of this problem implies the polynomial solvability of the representation conversion problem for general convex polytopes (i.e. the vertex enumeration and the facet enumeration problems). Here the polynomial solvability of the representation conversion problem means the existence of an algorithm that generates the second minimal representation in time polynomial in the size of both input and output. See Section 2.15 for discussion on complexity measures.

How does the above reduction work? Assume we have a polynomial algorithm for the verification, and we design an algorithm to generate all vertices of an H-polytope $P_H$. Let $V$ be a set of vertices of $P_H$ generated so far. Take the first inequality from the H-representation, and ask whether we have generated all vertices on the face $F_1$, the intersection of $P_H$ and the hyperplane given by the first inequality being forced to be equality. This is just one application of the verification algorithm. If yes, we move to the second inequality and repeat. Otherwise, we go down to lower dimensional face by setting one of the remaining inequality to equality. When we have $d$-independent equalities, we compute the unique vertex by solving the equation system. The key observation is that we generate a subproblem only when the verification algorithm returns NO answer. This means every subproblem created generates at least one new vertex. This guarantees our generation algorithm to be polynomial.

I do not know who is the first to recognize this reduction. I consider this belongs to folklore.

Finally I repeat: the complexity of the polyhedral verification problem is unknown. Is it in P or in coNP-complete? This is perhaps the most important question in polyhedral computation. A fascinating question, indeed.

2.19 Is there an efficient way of determining whether a given point $q$ is in the convex hull of a given finite set $S$ of points in $R^d$?

Yes. However, we need to be careful.

First we give a method that we do not recommend but many people use. This method computes an inequality representation $\{x\in R^d:\mathit{Ax}\le b\}$ of $\mathit{conv}(S)$ where $A$ is some $m\times d$ matrix and $b$ is a $m$-vector. This is called the convex hull computation 2.10. Once the system $\mathit{Ax}\le b$ is computed, it is easy to check whether $p$ satisfies the system or not.

In most cases, this method is too expensive, since the convex hull computation is very hard in general and impossible for large data. In fact, the number of inequalities in such a system $\mathit{Ax}\le b$ is often exponential in $d$ and $n=\left|S\right|$. (This method might be of practical interests when we need to remove lots of redundant points in clouds of points in small dimensions, see 2.20.)

A standard method to check whether $q$ is in $\mathit{conv}(S)$ uses linear programming (LP) technique 4. An LP problem to be formulated for the question is the following. Let $S=\{p_1,p_2,\dots <!--\; FUNCTION\; APPLICATION\; -->,p_n\}$.

This problem has no objective function and such a problem is often called a linear feasibility problem. Although it might look simpler problem to solve, it is polynomially equivalent to the general LP. In fact, it is usually a good idea to set up an equivalent LP to solve it. More specifically, the problem (4) has a solution if and only if the following has no solution:

Geometrically, the meaning of this problem is simple. If it admits a solution $(z_0,z)$, then the set $H=\{x\in R^d:z^{T}x=z_0\}$ is a hyperplane in $R^d$ separating the polytope $\mathit{conv}(S)$ from the inquiry point $q$. Thus the existence of the separation means the nonredundancy. Now, to actually solve the problem (5), we set up the LP:

The last inequality is artificially added so that the LP has a bounded solution. It is easy to see that the point $q$ is non-redundant if and only if the optimal value $f^{\ast }$ of the LP (6) is (strictly) positive.

2.20 How can one remove all interior points of $\mathit{conv}(S)$ from $S$ for large clouds $S$ of points in $R^d$?

The problem is formally known as the redundancy removal. Let $S$ be a set of $n$ points in $R^d$. We say a point $q\in S$ is redundant (for $\mathit{conv}(S)$) if $q\in \mathit{conv}(S-q)$. In short, redundant points are unnecessary to determine the convex hull $\mathit{conv}(S)$.

In principle, one can apply the linear programming (LP) method given in 2.19 to remove all redundant points. This amounts to solving $n$ LPs. While the time complexity of this pure LP method is polynomial and additional techniques given by [Cla94, OSS95] can reduce the size of LPs, this might end up in a very time consuming job for large $n$ (say $>1,000$).

We have recently tested Clarkson’s algorithm [Cla94] experimentally. Initial results posted in https://people.inf.ethz.ch/fukudak/ClarksonExp/ExperimentCube.html
indicate a huge acceleration for highly redundant cases.

There is a technique that might be useful to remove “obviously redundant” points quickly as a preprocessing. This works only in small dimensions (probably up to $100$?). Such a method picks up a few nonredundant point set $T=\{t_1,\dots <!--\; FUNCTION\; APPLICATION\; -->,t_k\}$ from $S$. Selecting nonredundant points can be done by picking points maximizing (or minimizing) any given linear function over $S$. When $k$ is small relative to $d$, say $d+2$ or $d+3$, the computation of $\mathit{conv}(T)$ is usually very easy with any standard convex hull algorithm. Thus we assume that an inequality system $\mathit{Ax}\le b$ such that $\mathit{conv}(T)=\{x:\mathit{Ax}\le b\}$ is given. It is easy to see that any point $q\in S-T$ satisfying the inequalities (i.e. $\mathit{Aq}\le b$) is redundant. One can repeat the same procedure with a different set $T^{\prime }$ of nonredundant points as long as it removes “sufficient number” of redundant points.

2.21 Is there any efficient algorithm to remove redundant inequalities from a system of linear inequalities

This problem is essentially equivalent to the redundancy removal from point sets given in 2.20.

Although one can transform one to the other, let us describe a direct method. Let $\mathit{Ax}\le b,s^{T}x\le t$ be a given system of $m$-inequalities in $d$-variables $x={(x_1,x_2,\dots <!--\; FUNCTION\; APPLICATION\; -->,x_d)}^T$. We want to test whether the subsystem of first $m-1$ inequalities $\mathit{Ax}\le b$ implies the last inequality $s^{T}x\le t$. If so, the inequality $s^{T}x\le t$ is redundant and can be removed from the system. A linear programming (LP) formulation of this checking is rather straightforward:

Then the inequality $s^{T}x\le t$ is redundant if and only if the optimal value $f^{\ast }$ is less than or equal to $t$.

By successively solving this LP for each untested inequality against the remaining, one would finally obtain a equivalent non-redundant system.

As we discussed in 2.20, there is a very promising idea to improve the naive LP technique above. It is proposed by Clarkson [Cla94] . The main idea is the following. Let’s denote by $m^{\prime }$ the number of nonredundant constraints which is not known in advance. Clarkson’s algorithm uses the same LP technique but for a subsystem $A^{\prime }x\le b^{\prime }$ of $\mathit{Ax}\le b$ of size at most $m^{\prime }$.

The subsystem is the currently recognized system of nonredundant constraints at some stage. If the tested inequality is redundant for this subsystem, then obviously it is redundant for the whole system. What can we do if the tested inequality is nonredundant? There is a so called “ray-shooting” technique that will find a new nonredundant inequality. The detailed discussion can be found in the textbook [Fuk20b, Chap 7].

We have tested Clarkson’s algorithm [Cla94] experimentally. Initial results posted in https://people.inf.ethz.ch/fukudak/ClarksonExp/ExperimentCube.html
indicate a huge acceleration for highly redundant cases.

2.22 Is there any efficient algorithm to compute the intersection of two (or $k$) polytopes

Let $k\ge 2$, and let $P_1,\dots <!--\; FUNCTION\; APPLICATION\; -->,P_k$ be input polytopes in $R^d$, and let $P=P_1\cap P_2\cap \cdots \cap P_k$ be the polytope we want to compute.

This problem of computing $P$ needs to be specified further. Namely, what is the representation of input and that of output?

If the input polytopes are H-polytopes (given by inequalities) then the intersection is represented by the union of the two inequality systems. To get a minimal H-reprentation for the intersection is just a redundancy removal given in Section 2.21. To get a minimal V-representation for the intersection is the vertex enumeration problem explained in Section 2.12.

An interesting case is when both input and output polytopes are V-polytopes (i.e. given by vertices and perhaps some redundant points). One primitive way to solve this problem consists of two steps: (1) generate minimal H-representations of each of the input $k$ polytopes, (2) solve the vertex enumeration problem for the union of the $k$ H-representations. This naive approach might be satisfactory for small dimensions or not-too-complicated polytopes. Recently, a polynomial algorithm has been found for the special case when the input polyopes are in general position [FLL00]. This algorithm is not yet practical because the general position assumption does not seem to be easily simulated for the general case. It should be remarked that the dual version of this problem is to compute a minimal H-representation of the convex hull of $k$ H-polytopes. Actually the paper [FLL00] treats this dual problem.

2.23 Is there any efficient algorithm to compute the volume of a convex polytope in $R^d$?

It is known that computing the volume of a $V$-polytope (or H-polytope) is #P-hard, see [DF88] and [Kha93]. There are theoretically efficient randomized algorithms to approximate the volume of a convex body [LS93] but no implementation seems to be available.

There is a comparative study [BEF00] of various volume computation algorithms for convex polytopes. It indicates that there is no single algorithm that works well for many different types of polytopes. For “near” simple polytopes, triangulation-based algorithms are more efficient. For “near” simplicial polytopes, sign-decomposition-based algorithms are better. See the paper for the justification of these claims.

3 Voronoi Diagram and Delaunay Triangulation

3.1 What is cell complex? What is triangulation?

A cell complex or simply complex in $R^d$ is a set $K$ of convex polyhedra (called cells) in $R^d$ satisfying two conditions: (1) Every face of a cell is a cell (i.e. in $K$), and (2) If $P$ and $P^{\prime }$ are cells, then their intersection is a common face of both. A simplicial complex is a cell complex whose cells are all simplices.

The body $\left|K\right|$ of a complex $K$ is the union of all cells. When a subset $P$ of $R^d$ is the body of a simplicial complex $K$, then $K$ is said to be a triangulation of $P$. For a finite set $S$ of points in $R^d$, a triangulation of $S$ is a simplicial complex $K$ with $\left|K\right|=\mathit{conv}(S)$.

3.2 What is Voronoi diagram in $R^d$?

See also 3.3.

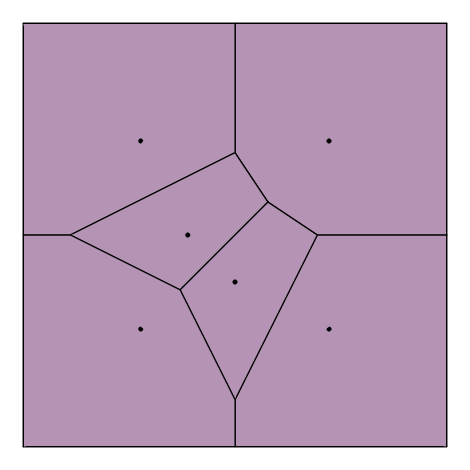
Given a set $S$ of $n$ distinct points in $R^d$, Voronoi diagram is the partition of $R^d$ into $n$ polyhedral regions $\mathit{vo}(p)$ ($p\in S$). Each region $\mathit{vo}(p)$, called the Voronoi cell of $p$, is defined as the set of points in $R^d$ which are closer to $p$ than to any other points in $S$, or more precisely,

where $\mathit{dist}$ is the Euclidean distance function. (One can use different distance functions to define various variations of Voronoi diagrams, but we do not discuss them here.)

The set of all Voronoi cells and their faces forms a cell complex. The vertices of this complex are called the Voronoi vertices, and the extreme rays (i.e. unbounded edges) are the Voronoi rays. For each point $v\in R^d$, the nearest neighbor set $\mathit{nb}(S,v)$ of $v$ in $S$ is the set of points $p\in S-v$ which are closest to $v$ in Euclidean distance. Alternatively, one can define a point $v\in R^d$ to be a Voronoi vertex of $S$ if $\mathit{nb}(S,v)$ is maximal over all nearest neighbor sets.

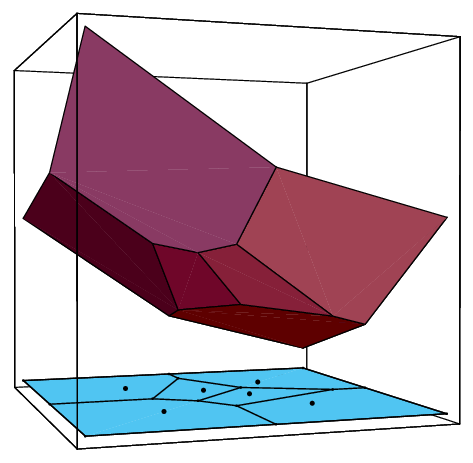
In order to compute the Voronoi diagram, the following construction is very important. For each point $p$ in $S$, consider the hyperplane tangent to the paraboloid in $R^{d+1}$ at $p$: $x_{d+1}=x_1^2+\cdots +x_d^2$. This hyperplane is represented by $h(p)$:

By replacing the equality with inequality $\ge$ above for each point $p$, we obtain the system of $n$ inequalities, which we denote by $b-\mathit{Ax}\ge 0$. The polyhedron $P$ in $R^{d+1}$ of all solutions $x$ to the system of inequalities is a lifting of the Voronoi diagram to one higher dimensional space. In other words, by projecting the polyhedron $P$ onto the original $R^d$ space, we obtain the Voronoi diagram in the sense that the projection of each facet of $P$ associated with $p\in S$ is exactly the voronoi cell $\mathit{vo}(p)$. The vertices and the extreme rays of $P$ project exactly to the Voronoi vertices and the rays, respectively.

3.3 What is the Delaunay triangulation in $R^d$?

See also 3.2, 3.1.

Let $S$ be a set of $n$ points in $R^d$. The convex hull $\mathit{conv}(\mathit{nb}(S,v))$ of the nearest neighbor set of a Voronoi vertex $v$ is called the Delaunay cell of $v$. The Delaunay complex (or triangulation) of $S$ is a partition of the convex hull $\mathit{conv}(S)$ into the Delaunay cells of Voronoi vertices together with their faces.

The Delaunay complex is not in general a triangulation but becomes a triangulation when the input points are in general position (or nondegenerate), i.e. no $d+2$ points are cospherical or equivalently there is no point $c\in R^d$ whose nearest neighbor set has more than $d+1$ elements.

The Delaunay complex is dual to the Voronoi diagram 3.2 in the sense that there is a natural bijection between the two complexes which reverses the face inclusions.

There is a direct way to represent the Delaunay complex, just like the Voronoi diagram 3.2. In fact, it uses the same paraboloid in $R^{d+1}$: $x_{d+1}=x_1^2+\cdots +x_d^2$. Let $f(x)=x_1^2+\cdots +x_d^2$, and let $\stackrel{}{p~}=(p,f(x))\in R^{d+1}$ for $p\in S$. Then the so-called lower hull of the lifted points $\stackrel{}{S~}:=\{\stackrel{}{p~}:p\in S\}$ represents the Delaunay complex. More precisely, let

where $e^{d+1}$ is the unit vector in $R^{d+1}$ whose last component is $1$. Thus $P$ is the unbounded convex polyhedron consisting of $\mathit{conv}(\stackrel{}{S~})$ and any nonnegative shifts by the “upper” direction $r$. The nontrivial claim is that the the boundary complex of $P$ projects to the Delaunay complex: any facet of $P$ which is not parallel to the vertical direction $r$ is a Delaunay cell once its last coordinate is ignored, and any Delaunay cell is represented this way.

3.4 Computing the Delaunay complex and the Voronoi diagram. What does it mean and how to do it with available software?

Let $S$ be a given set of $n$ points in $R^d$. Computing the Voronoi diagram normally means to generate the set $Vo(S)$ of Voronoi vertices, and computing the Delaunay complex is essentially the same thing. Once the Voronoi vertices are generated, the nearest neighbor sets $\mathit{nb}(S,v)$ for all Voronoi vertices $v$ can be easily computed, and in fact most of the algorithms for generating the Voronoi vertices computes the nearest neighbor sets as well at the same time.

The complexity of computing the Voronoi diagram is not well understood in general. For example, there is no known algorithm that runs polynomial in the size of input and output. For the much easier nondegenerate case, there is an algorithm, known as the reverse search algorithm, which runs in time $O(\mathit{nd}|Vo(S)|)$. When the dimension is fixed (in particular $d=2$), one can analyse complexities of various-type algorithms in terms of the input size. In the plane, there are $O(n\log <!--\; FUNCTION\; APPLICATION\; -->n)$ algorithms that is optimal, and for fixed $d$ there is an incremental $O(n^{\lceil d∕2\rceil })$ algorithm, see [Ge97, Chapter 20].

How large is the number $|Vo(S)|$ of output? The tight upper bound was given in [Sei91] which is $O(n^{\lfloor (d+1)∕2\rfloor })$. While this bound may be a far over-estimate of expected behavior, the number of output typically grows exponentially in $n$ and $d$, and thus the computation itself is expected to be heavy. Therefore, one must take a caution to do the Delaunay/Voronoi computation. In fact,

I know quite a few people who tried to use Voronoi diagram computation codes in order to accomplish a much simpler task.

It is not only a waste of time and computer resources, but it often leads to a prohibitively hard computation, while an appropriate use of mathematical techniques resolves the problem instantly.

For example, the following computations are much simpler and should be solved via linear programming techniques in Section 4:

• For given two points $p$ and $q$ in $S$, check whether their Voronoi cells are adjacent in the Voronoi diagram, see 3.5.
• For any given point $c\in R^d$, find a Delaunay cell containing $c$, see 3.7.

The most natural way to compute the Voronoi diagram is by computing the vertices and the extreme rays of the polyhedron in $R^{d+1}$ given in 3.2. By ignoring the last component of each vertices we obtain the Voronoi vertices.

3.4.1 Sample session with cddlib

Consider a simple two dimensional case: $d=2$, $n=6$ and $S=\{(0,0),(2,1),(1,2),(4,0),(0,4),(4,4)\}$. In principle the session below will work in any $d$ and $n$, although the computation time depends heavily on the size.

The first step is to write down the system of linear inequalities in $(d+1)$ variables as explained in 3.2: for each $p\in S$,

For our example, we have:

We denote by $P$ the polyhedron of all solutions $x\in R^d$ satisfying the inequalities above. Now we prepare an input file for cddlib. The file must be in polyhedra format and for the system above, it is rather straightforward since it essentially codes the coefficients of the system.

* filename: vtest_vo.ine
H-representation
begin
 6   4   integer
  0  0  0  1
  5 -4 -2  1
  5 -2 -4  1
 16 -8  0  1
 16  0 -8  1
 32 -8 -8  1
end
incidence
input_adjacency

The last two lines “incidence” and “input_adjacency” are options for the (old) standalone code cdd+. They are not necessary for scdd.c (a sample code for cddlib). The executables of scdd.c, namely, scdd (floating-point) or scdd_gmp (gmp exact rational) computes the second (generator) representation vtest_vo.ext of the polyhedron and output four files vtest_vo.icd, vtest_ecd, vo.vtest_vo.iad, and vtest_vo.ead.

Now, by running scdd.c with commands:

% scdd_gmp vtest_vo.ine

or

% scdd vtest_vo.ine

we obtain the five files mentioned above. Among them the most important for our purpose are the following three, vtest_vo.ext (all extreme points and rays), vtest_vo.iad (adjacency of facet inequalities) and vtest_vo.ecd (incidence of extreme points/rays and inequalities). Note that scdd_gmp runs in rational exact arithmetic and scdd runs in floating-point arithmetic. scdd runs much faster than scdd_gmp but it may not give a correct answer.

The file vtest_vo.ext would be something like the following:

___________________________________________________________________________________________

ext_file: Generators
V-representation
begin
 10 4 rational
 0 -1 0 0
 1 -3/2 2 0
 1 5/6 5/6 0
 1 2 -3/2 0
 0 0 -1 0
 1 27/10 27/10 56/5
 1 15/4 2 14
 0 1 0 8
 0 0 1 8
 1 2 15/4 14
end

___________________________________________________________________________________

The output contains all the vertices and extreme rays of the (unbounded) polyhedron $P$ in $R^3$. Namely each row starting with “1” represents a vertex. So the second row

  1 -3/2 2 0

represents the vertex $(-3∕2,2,0)$. Each row starting with “0” represents an extreme ray, e.g. the first row

  0 -1 0 0 

represents the ray $(-1,0,0)$.

By ignoring the last components, we obtain the set of six Voronoi vertices $(-3∕2,2)$, $(5∕6,5∕6)$, $(2,-3∕2)$, $(27∕10,27∕10)$, $(15∕4,2)$ and $(2,15∕4)$ and four Voronoi rays $(-1,0)$, $(0,-1)$, $(1,0)$ and $(0,1)$.

The incidence file vtest_vo.ecd file:

___________________________________________________________________________________________

ecd_file: Incidence of generators and inequalities
begin
  10    7
 1 3 : 1 5 7
 2 3 : 1 3 5
 3 3 : 1 2 3
 4 3 : 1 2 4
 5 3 : 1 4 7
 6 3 : 2 3 6
 7 3 : 2 4 6
 8 3 : 4 6 7
 9 3 : 5 6 7
 10 3 : 3 5 6
end

___________________________________________________________________________________

Each row corresponds to the same row in vtest_vo.ext file. For example, the second data

 2 3 : 1 3 5

says the second data in vtest_vo.ext file:

 1 -3/2 2 0

is a voronoi vertex whose nearest neighbor set is $\{p^1,p^3,p^5\}$. Also, this set corresponds to a Delaunay cell. Similarly, the first row

 1 3 : 1 5 7

indicates the ray (the first output in vtest_vo.ext file)

  0 -1 0 0 

is determined by 1, 5 and 7th halfspaces. The 7th halfspace is an artificial one corresponding to the infinity. So this ray is determined by the input points 1 and 5 and going to infinity.

Thus, the index sets (triples, in this case) not containing the infinity $7$ determine all Delaunay cells, and those containing $7$ correspond to the Voronoi rays.

Finally, look at the vtest_vo.iad file:

___________________________________________________________________________________________

iad_file: Adjacency of inequalities
begin
  7    7
 1 -5 : 1 6
 2 -4 : 2 5 7
 3 -4 : 3 4 7
 4 -4 : 3 4 5
 5 -4 : 2 4 5
 6 -5 : 1 6
 7 -4 : 2 3 7
end

___________________________________________________________________________________

This file contains the graph structure (adjacency list) of the Delaunay complex and equivalently the adjacency of Voronoi cells in the Voronoi diagram.

For example, the first row

  1 -5 : 1 6

says that the first Voronoi cell is adjacent to $5$ cells. The row is equivalent to

  1 5 : 2 3 4 5 7

Notice that the cddlib lists the non-neighbors whenever the number of non-neighbors is smaller than that of neighbors. Thus, the negative $-5$ indicates that the list is non-neighbors.

In the language of the Delaunay complex, the first line in this file says the point $p^1$ is adjacent to $5$ neighbors $p^2$, $p^3$, $p^4$, $p^5$ and $p^7$. Here, the point $p^7$ is the artificial infinity point which is considered adjacent to any input point whose Voronoi cell is unbounded.

As we remarked before, this graph information can be computed much more efficiently by linear programming. See 3.5.

3.5 Is it possible to compute only the adjacencies of Voronoi cells in the Voronoi diagram efficiently?

Yes, it can be done very efficiently by linear programming (LP), and very importantly this can be done for very large scale problems, with practically no bounds on the size with an efficient LP solver.

The method is simple. The lifting technique we described in 3.2 immediately gives the idea. Recall that the Voronoi diagram of a set $S$ of $n$ points in $R^d$ is the projection of the following $(d+1)$-polyhedron to $R^d$ space of the first $d$ components.

For simplicity, denote it as

where $A$ is a given $n\times (d+1)$ matrix and $b$ is a $n$-vector. Now for each $i=1,\dots <!--\; FUNCTION\; APPLICATION\; -->,n$, consider the $i$th facet $F_i$ of $P$:

Two facets $F_i$ and $F_j$ are called adjacent if the intersection $F_i\cap F_j$ is a facet of both, i.e. has dimension $d-2$. An equivalent definition is: they are adjacent if (*) the facet $F_i$ becomes larger once the facet $F_j$ is removed from the polyhedron, i.e. the $j$th inequality is removed from the system $b-Ax\ge 0$.

It is easy to see that two Voronoi cells $\mathit{vo}(p^i)$ and $\mathit{vo}(p^j)$ are adjacent if and only if the corresponding facets $F_i$ and $F_j$ are adjacent in the polyhedron $P$. Now, we formulate the following LP for any distinct $i$, $j=1,2,\dots <!--\; FUNCTION\; APPLICATION\; -->,n$:

where $b^{\prime }$ is equal to $b$ except for $j$th component $b_j^{\prime }=b_j+1$. The new inequality system $b^{\prime }-Ax\ge 0$ is simply a modification of the original system obtained by relaxing the $j$th inequality a little bit. An important remark is, by definition (*), $F_j$ and $F_i$ are adjacent if and only if the objective value $f(x)$ is negative at an optimum solution. Thus we formulated the Voronoi adjacency computation as an LP problem.

How much do we gain by using LP for the adjacency computation, instead of computing the whole Voronoi diagram? A lot. It is hard to exaggerate this, because the LP (10) (in fact any LP) is solvable in polynomial time, whereas the associated Voronoi computation is exponential in $d$ and $n$. Using the standard simplex method, the time complexity of solving an LP is not polynomial, but the practical complexity is roughly $O(n{d}^3)$.

3.5.1 Sample session with cddlib

With cddlib, a setup for computing the adjacency of Voronoi cells is quite simple. Consider the same example 3.4.1. For each input point $i=1,2,3,4,5,6$, we write the inequality system for the facet $F_i$:

instead of writing the relaxed inequality (10). For example, for $i=4$, we have

___________________________________________________________________________________________

H-representation
begin
 7   4   real
  0  0  0  1
  5 -4 -2  1
  5 -2 -4  1
 16 -8  0  1
 16  0 -8  1
 32 -8 -8  1
-16  8  0 -1
end
facet_listing

___________________________________________________________________________________

We save this as the file vtest_vof4.ine The last inequality is the negative of the forth inequality to force the forth inequality to be equality.

The old code cdd+ accepts an option called “facet_listing”. With this option, cdd+ will check which of the given inequalities is redundant or not (essential), by solving the associated LP’s (10) for each inequality $j$.

With cddlib, we can do the same test by the program redcheck.c, which is distributed in the src subdirectory. This program ignores this option line, and does the redundancy removal and finds a minimal representation of the polyhedron.

By running the executable redcheck_gmp (exact gmp rational) or redcheck (floating-point) by

% redcheck_gmp vtest_vof4.ine

we will get the output:

___________________________________________________________________________________________

input file vtest_vof4.ine is open
Canonicalize the matrix.
Implicit linearity rows are: 4 7

Redundant rows are: 3 5

Nonredundant representation:
The new row positions are as follows (orig:new).
Each redundant row has the new number 0.
Each deleted duplicated row has a number nagative of the row that
represents its equivalence class.
 1:2 2:3 3:0 4:1 5:0 6:4 7:0
H-representation
linearity 1  1
begin
 4 4 rational
 16 -8 0 1
 0 0 0 1
 5 -4 -2 1
 32 -8 -8 1
end

___________________________________________________________________________________

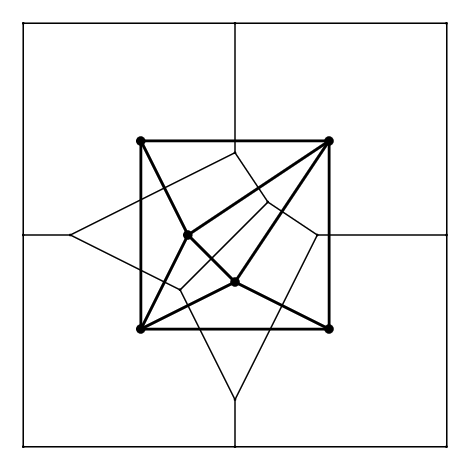
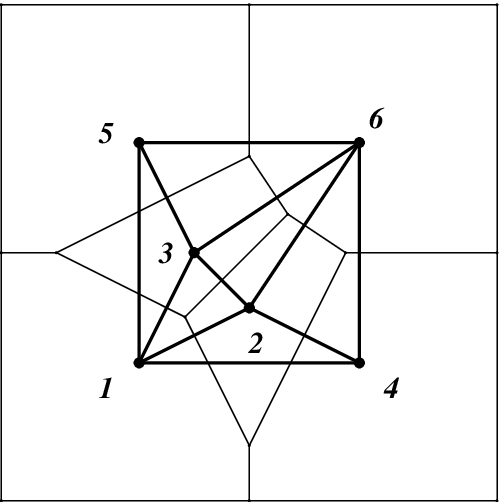
First of all, it recognizes that the $4$th and the $7$th row are implicit equations and should be written as an equation. Then, the redundant rows are recognized as $3$rd and $5$th. Thus, we can consider the set $\{1,2,6\}$ as the indices of essential constraints, or equivalently the indices of Voronoi cells adjacent to the $4$th cell. Of course, this adjacency coincides with the adjacency of input points in the Delaunay triangulation. See the figure below.

3.6 Is it possible to compute only the edges of the Delaunay complex (triangulation) ?

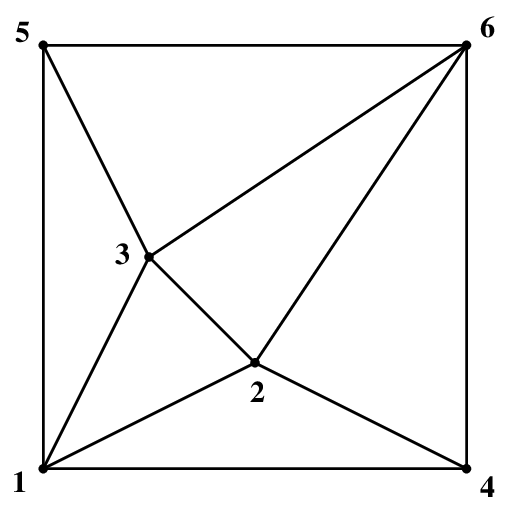
This is essentially the same question as computing the adjacencies of Voronoi cells, see 3.5.

3.7 Is it possible to determine the Delaunay cell containing a given point efficiently?

Yes, it is possible to find the nearest point set associated with the Delaunay cell containing a given point $c\in R^d$. As we discussed in Section 3.3, the Delaunay complex can be represented by the convex hull of appropriately lifted points in $R^{d+1}$, and the non-vertical facets coincide with the Delaunay cells once they are projected to the original space. Thus the problem of determining the Delaunay cell containing a given point $c$ can be reduced to finding the first facet of a polyhedron “shoot” by a ray.

To be more precise, let $f(x)=x_1^2+\cdots +x_d^2$, and let $\stackrel{}{p~}=(p,f(x))\in R^{d+1}$ for $p\in S$. Then the lower hull $P$ of the lifted points $\stackrel{}{S~}:=\{\stackrel{}{p~}:p\in S\}$:

represents the Delaunay complex. Here $e^{d+1}$ is the unit vetor in $R^{d+1}$ whose last component is $1$. For any vector $ỹ\in R^{d+1}$ and $y_0\in R$, let ${ỹ}^{T}x\ge -y_0$ denote a general inequality of a variable vector $x\in R^{d+1}$. For such an inequality to represent a valid inequality of $P$ (see Section 2.2), it must be satisfied by all points in $\stackrel{}{S~}$:

and by any points shifted vertically upwards, i.e.

Under the first inequality (11), the last inequality is equivalent to

Now every Delaunay cell is a projection of a non-vertical facet of $P$. We are thus looking for an inequality ${ỹ}^{T}x\ge -y_0$ satisfying (11), (12) and $y_{d+1}\ne 0$. By scaling with ${ỹ}_{d+1}>0$, we may assume ${ỹ}_{d+1}=1$. For a given point $c$, let $\stackrel{}{c~}={(c,0)}^T$, and let $L(\lambda )=\stackrel{}{c~}+\lambda e^{d+1}$, $\lambda \ge 0$. Determining the Delaunay cell containing $c$ is equivalent to finding the last inequality “hit” by the halfline $L$. More precisely, it is to find a non-vertical facet inequality such that the intersecion point of the corresponding hyperplane $\{x:y^{T}x=-y_0\}$ and the half line $L(\lambda ),\lambda \ge 0$ is highest possible.

By substituting $L(\lambda )$ for $x$ in $y^{T}x=-y_0$ with ${ỹ}_{d+1}=1$, we obtain

where $y$ denotes the vector $ỹ$ without the last coordinate ${ỹ}_{d+1}$. The LP formulation is therefore:

While an optimal solution $(y_0,y)$ to this LP may not determine any facet in general, the simplex method always returns an optimal basic solution which determines a facet inequality in this case. The Delaunay cell containing $c$ is the one determined by the set of points in $S$ whose corresponding inequalities are satisfied by equality at the optimal solution. If the LP solution is not degenerate, the dual variables that are positive at the dual optimal solution coincides with the former set.

It is important to note that the above LP might be unbounded. If it is unbounded, it can be easily shown that $c$ is not in any Delaunay cell, i.e., not in the convex hull of $S$. A certificate of unboundedness actually induces a hyperplane strongly separating $c$ from $S$. (why?)

3.7.1 Sample session with cddlib

With cddlib (scdd.c) and any reasonable LP code, the only necessary step should be to prepare the LP file for determination of the Delaunay cell containing a given point $c\in R^d$. Consider the same example 3.4.1.

For a given point $c=(3,2)$, the LP (13) file for scdd or scdd_gmp is

___________________________________________________________________________________________

H-representation
begin
  6  4  rational
  0  1  0  0
  5  1  2  1
  5  1  1  2
 16  1  4  0
 16  1  0  4
 32  1  4  4
end
minimize
  0  1  3  2

___________________________________________________________________________________

The solution by scdd_gmp is:

___________________________________________________________________________________________

* #constraints = 6
* #variables   = 3
* Algorithm: dual simplex algorithm
* minimization is chosen
* Objective function is
 0 + 1 X[  1] + 3 X[  2] + 2 X[  3]
* LP status: a dual pair (x,y) of optimal solutions found.
begin
  primal_solution
    1 :  14
    2 :  -15/2
    3 :  -4
  dual_solution
    2 :  -1/2
    4 :  -1/8
    6 :  -3/8
  optimal_value :  -33/2
end

___________________________________________________________________________________

Therefore, the facet inequality is $14-15∕2x_1-4x_2\ge 0$, and the dual solution indicates that the points $p^2,p^4,p^6$ determine the Delaunay cell which contains $(3,2)$.

3.8 What is the best upper bound of the numbers of simplices in the Delaunay triangulation?

See 3.4.

4 Linear Programming

4.1 What is LP?

A linear programming (abbreviated by LP) is to find a maximizer or minimizer of a linear function subject to linear inequality constraints. More precisely,

Theoretically every rational LP is solvable in polynomial time by both the ellipsoid method of Khachian (see [Kha79, Sch86]) various interior point methods (see [Kar84, RTV97]). The well-known simplex method of Dantzig (see [Dan63, Chv83]) has no known polynomial variants. In practice, very large LPs can be solved efficiently by both the simplex method and interior-point methods. For example, it is very easy on a standard unix station to solve an LP with $d=100$ and $m=100,000$, while the vertex enumeration/convex hull computation of the same size is simply intractable. There are many commercial codes and public codes available. See the LP FAQ [FG]. Two excellent classical books on LP are Chvatal’s textbook [Chv83] and Schrijver’s “researcher’s bible” [Sch86].

There is a new textbook on LP theory and Optimization [Fuk20a] which explains the duality theory and the finite pivoting theory quite differently from the classical textbooks. One essential difference comes from a rather elementary fact that the classical numbering of the dual variables is not mathematically sound, see [Fuk20a, Chap 1–4]. Once the dual variables are properly renumbered, one can see that the LP duality is a property of the orthogonal dual pairs of vector subspaces of $R^n$.

5 Polyhedral Computation Codes

• cddlib, cdd and cdd+ [Fuka] (C and C++ implementations of the double description method [MRTT53]).

  Comments: Runs on both floating and exact arithmetic. Efficient for highly degenerate cases. The exact versions are much slower. It can remove redundancies from input data using a built-in LP code. cddlib is a C-library with basic polyhedral conversion functions and LP solvers. cddlib can be compiled with both GMP rational (mpq) and floating point arithmetic. A new arithmetic (with an arithmetic library) can be added to cddlib.

• lrs and lrslib [Avi] (C implementation of the reverse search algorithm [AF92]). A parallel version prs was developed by A. Marzetta, see [BMFN96].

  Comments: Exact arithmetic only, efficient for nondegenerate cases. Uses a little memory and perhaps the only available code which can deal with problems in high dimensions, say, over $20$. There is a parallel implementation mplrs that uses the MPI library.

• pd [Mar97] (C implementation of the primal-dual algorithm [BFM97]).

  Comments: Exact arithmetic only, efficient for dually nondegenerate cases.

• qhull [BDH96, BDH03] (C implementation of the beneath-beyond method, see [Ede87, Mul94], which is a sort of dual of the double description method).

  Comments: Floating arithmetic only but handles numerical problems well. Highly efficient for nondegenerate cases. User can call it as a C-libary.

• porta [CL97] (C implementation of the Fourier-Motzkin elimination method [Zie94]).

  Comments: Efficient for combinatorial (e.g. 0-1) polytopes. Guarantees correct numerical results as long as double precision integer arithmetic does not overflow. It can list all integer solutions in a polytope.

• polymake [GJ99] (computational environment for the algorithmic treatment of polytopes and polyhedra).

  One can generate convex polytopes and do various computations with convex polyhedra. It uses cddlib/porta/lrslib for representation conversions. It is extendable by writing own ”rules” to generate new structures/data associated with polyhedra.

• PPL [Bag04] (C++ implementation of the double description method [MRTT53]).

  Comments: A modern efficient implementation. Exact arithmetic only.

• zeRone [Lüb99] (C implementation of the backtrack vertex enumeration algorithm for 0-1 H-polytopes [BL98].

  Comments: In general, the straightforward backtrack algorithm for the vertex enumeration problem must solve NP-complete decision problems, as it was shown in [FLM97]. The situation is different for 0-1 polytopes and the problem is strongly polynomially solvable. The code can generate all 0-1 points in a general H-polytope. It relies on the commercial LP solver CPLEX.

• Pointers to many other programs in geometric computations are stored in [Ame, Eri].
• For linear programming, one should check the Linear Programming FAQ at [FG]. It lists both public (open source) and commercial codes.

6 Acknowledgements

The author expresses his sincere thanks to Dr. Vera Rosta who read an earlier version of FAQ carefully, found numerous errors and provided with many helpful suggestions.

References